 \(\fbox{例1}\)
\(\fbox{例1}\)
已知函数\(f(x)=-x^2+2ex+m-1,g(x)=x+\cfrac{e^2}{x}(x>0)\).
(1)若\(y=g(x)-m\)有零点,求\(m\)的取值范围;
(2)确定\(m\)的取值范围,使得\(g(x)-f(x)=0\)有两个相异实根.
解析:(1) 因为\(g(x)=x+\cfrac{e^2}{x}\ge 2\sqrt{e^2}=2e\),等号成立的条件是\(x=e\),
故\(g(x)\)的值域是\([2e,+\infty)\),
因而只需\(m≥2e\),则\(y=g(x)-m\)就有零点。
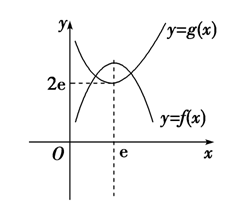
(2) 若\(g(x)-f(x)=0\)有两个相异实根,即\(g(x)\)与\(f(x)\)的图像有两个不同的交点,
作出\(g(x)=x+\cfrac{e^2}{x}(x>0)\)的大致图像如图.
因为\(f(x)=-x^2+2ex+m-1=-(x-e)^2+m-1+e^2\).
所以其图像的对称轴为\(x=e\),开口向下,
最大值为\(m-1+e^2\),故当\(m-1+e^2>2e\),即\(m>-e^2+2e+1\)时,
\(g(x)\)与\(f(x)\)有两个交点,即\(g(x)-f(x)=0\)有两个相异实根,
所以\(m\)的取值范围是\((-e^2+2e+1,+\infty)\).
 \(\fbox{例2}\)
\(\fbox{例2}\)
函数\(f(x)=\begin{cases}x^2+4x,x\leq 0\\xlnx,x>0\end{cases}\),\(g(x)=kx-1\),若方程\(f(x)-g(x)=0\)在\(x\in(-2,2)\)有三个实根,则实数\(k\)的取值范围是【】
A.\((1,ln2\sqrt{e})\;\;\;\;\;\) B.\((ln2\sqrt{e},\cfrac{3}{2})\;\;\;\;\;\) C.\((\cfrac{3}{2},2)\;\;\;\;\;\) D.\((1,ln2\sqrt{e})\cup(\cfrac{3}{2},2)\;\;\;\;\;\)
分析:显然\(x=0\)不是方程\(f(x)-g(x)=0\)的根,故可变形为\(k=\cfrac{f(x)+1}{x}\),
设\(\phi(x)=\cfrac{f(x)+1}{x}=\begin{cases}x+\cfrac{1}{x}+4,x<0\\\cfrac{1}{x}+lnx,x>0\end{cases}\),即\(k=\phi(x)\)在\(x\in(-2,2)\)有三个实根,
用导数方法研究函数\(\phi(x)\)的单调性,做出其图像
由图像可得,要使得函数\(y=k\)与函数\(y=\phi(x)\)有三个交点,则\(k\in (1,ln2\sqrt{e})\cup(\cfrac{3}{2},2)\)
 \(\fbox{例3}\)
\(\fbox{例3}\)
若存在两个正实数\(x,y\),使得等式\(3x+a(2y-4ex)\cdot(lny-lnx)=0\)成立,其中\(e\)为自然对数的底数,则\(a\)的取值范围是__________。\((-\infty,0)\cup [\cfrac{3}{2e},+\infty)\)。
分析:由于\(x\neq 0\),故两边同时除以\(x\),二元变一元,变量集中,
得到\(3+a(2\cdot \cfrac{y}{x}-4e)\cdot ln\cfrac{y}{x}=0\),令\(\cfrac{y}{x}=t>0\),
则\(3+a(2t-4e)\cdot lnt=0\),即\(a(2t-4e)\cdot lnt=-3\),
由于\(a\neq 0\),则上式变形为\((2t-4e)\cdot lnt=-\cfrac{3}{a}\),
即存在正数\(t\),使得方程\((2t-4e)\cdot lnt=-\cfrac{3}{a}\)成立,
令\(g(t)=(2t-4e)\cdot lnt\),
例6若关于\(x\)的方程\((lnx-ax)lnx=x^2\)存在三个不等实根,则实数\(a\)的取值范围是_________。
分析:当\(x=1\)时,\(lnx=0\),原式不成立,故不可能;
当\(lnx\neq 0\)时,\(lnx-ax=\cfrac{x^2}{lnx}\),故\(ax=lnx-\cfrac{x^2}{lnx}\),分离参数得到,
则\(a=\cfrac{lnx}{x}-\cfrac{x}{lnx}\),令\(h(x)=\cfrac{lnx}{x}-\cfrac{x}{lnx}\),则\(y=a\)与\(y=h(x)\)的图像有三个交点,
\(h'(x)=\cfrac{\cfrac{1}{x}\cdot x-lnx}{x^2}-\cfrac{lnx-x\cdot \cfrac{1}{x}}{(lnx)^2}=\cfrac{1-lnx}{x^2}-\cfrac{lnx-1}{(lnx)^2}\),\(x>0\)且\(x\neq 1\),
当\(x\in (0,1)\)时,\(h'(x)>0\),故\(h(x)\)单调递增;
当\(x>1\)时,\(h'(x)=\cfrac{(1-lnx)(lnx)^2-(lnx-1)\cdot x^2}{x^2\cdot (lnx)^2}\)
\(=\cfrac{((lnx)^2+x^2)\cdot (1-lnx)}{x^2\cdot (lnx)^2}\)
当\(x\in (1,e)\)时,\(h'(x)>0\),\(h(x)\)单调递增,\(x\in (e,+\infty)\)时,\(h'(x)<0\),\(h(x)\)单调递减,
又\(h(e)=\cfrac{1}{e}-e\),做出大致图像如下:
要使得则\(y=a\)与\(y=h(x)\)的图像有三个交点,必须\(a<\cfrac{1}{e}-e\)。